I was asked to comment about how time dilation affected astronaut Scott Kelly during his “year in space,” leading to this article at the Huffington Post:
Neil DeGrasse Tyson Says Scott Kelly Aged More Slowly In Space, And He’s Right
We’ve got the math to prove it.
by: David Freeman

Astronaut Scott Kelly returned from nearly a year in space Tuesday with a certain youthful glow. (Photo by Bill Ingalls/NASA via Getty Images)
Astronaut Scott Kelly got countless “welcome home” messages on Twitter following his return to Earth Tuesday after spending almost a year in space.
But a tweet from Neil deGrasse Tyson stood out for referencing Albert Einstein’s theory of relativity — and for noting one particularly mind-bending implication it has for Kelly, given his long stint in orbit:
As the bearer of a Ph.D. in astrophysics from Columbia University, Tyson knows a thing or two about spaceflight and relativity. But is he correct that time passed more slowly for Kelly in space, thanks to what’s known as the time-dilation effect? And did he get the math right?
According to Dr. Jeffrey Bennett, a Colorado-based astrophysicist and author of the 2014 book What is Relativity?, Tyson nailed it.
“Relativity tells us that when we (in this case meaning all of us on Earth) observe someone/something else that is moving relative to us (in this case the International Space Station), we will see time running slower for the moving people/things,” Bennett told The Huffington Post in an email. “It’s called time ‘dilation’ because you can think of the moving person’s time as having ‘expanded’ (dilated) since less time passes for them than for us.”
Bennett said the following equation can be used to calculate the time dilation between Earth (the “rest frame” in the equation) and Kelly’s body aboard the ISS (the “moving frame”):
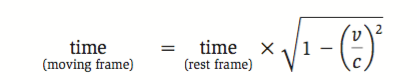
Bennett explained that the “v/c” term represents the space station’s speed (v) as a fraction of the speed of light (c). The space station’s orbital speed is about 17,000 miles per hour, Bennett said, or about 7.8 kilometers per second. The speed of light is 300,000 kilometers per second. So divide 7.8 by 300,000, and you get 0.000026.
To get the term on the equation’s right side, you square that number and subtract the result from 1. That gives you 0.9999999993. Take the square root of that number, and you get 0.9999999997.
So, one year in orbit is equivalent to 0.9999999997 years on Earth. Put another way: While the rest of us experienced a year on Earth, Kelly experienced just a tiny bit less than one full Earth year. Specifically, his year was shorter than ours by 0.0000000003 years, or roughly 0.01 seconds.
Just as Tyson said.
(Of course, one can always quibble. Bennett noted that a more precise calculation shows that Kelly aged less than us by 0.00946 seconds per year — and since he was in space for 340 days rather than 365, he really aged less than us by 0.0088 seconds during that period.)
As for why time dilates in this way, Bennett cited the principle of relativity that holds that space and time are closely intertwined, not two different things. Consequently, observers moving relative to one another will measure space and time differently.
The only thing that all observers agree on is the speed of light. Well, that and the fact that after almost a year in space, it’s good to be home.
